Ohjeita aineiston käytöstä eri tilasto-ohjelmistoissa
Tämän sivun sisältö
- Otanta-asetelma: ositus ja otoskoko
- Painokertoimien taustaa
- Painokerroinmuuttujat ja otanta-asetelman määrittäminen
- Perustunnusluvut
- Lineaarinen regressiomalli
- Waldin testi
- Logistinen regressiomalli
- Lopuksi
Otanta-asetelma: ositus ja otoskoko
- Kohdejoukko: 18–34-vuotiaat korkeakouluopiskelijat
- Korkeakouluittain ositettua satunnaisotanta, yhteensä noin 12 000 opiskelijaa (yliopisto 6 000 + ammattikorkeakoulu 6 000)
- Otannan korkeakoulukohtainen poimintatiheys: koulukohtainen otoskoko oli sitä suurempi, mitä enemmän kyseisessä korkeakoulussa on opiskelijoita, kuitenkin vähintään noin 150 ja enintään noin 400 amk-opiskelijaa / 800 yo-opiskelijaa jokaisesta korkeakoulusta
Painokertoimien taustaa: osituksen vaikutuksia
- Otoskoko suhteessa perusjoukon kokoon vaihtelee korkeakouluittain
- Yksilöillä erilaiset poimintatodennäköisyydet
- Suorat keskiarvot ovat virheellisiä → Painokertoimet
Painokertoimien taustaa: kato
- Yksilöiden osallistumisaktiivisuus vaihtelee
- Jos aktiivisuuteen vaikuttavat tekijät havaitaan sekä osallistuneista että katotapauksista erot voidaan korjata hyvin (esim. rekisteritiedot: ikä, sukupuoli, sektori…), taustalla oletus havaittujen ja katotapausten samankaltaisuudesta → Painokertoimet
Vastausaktiivisuuksia, KOTT 2021
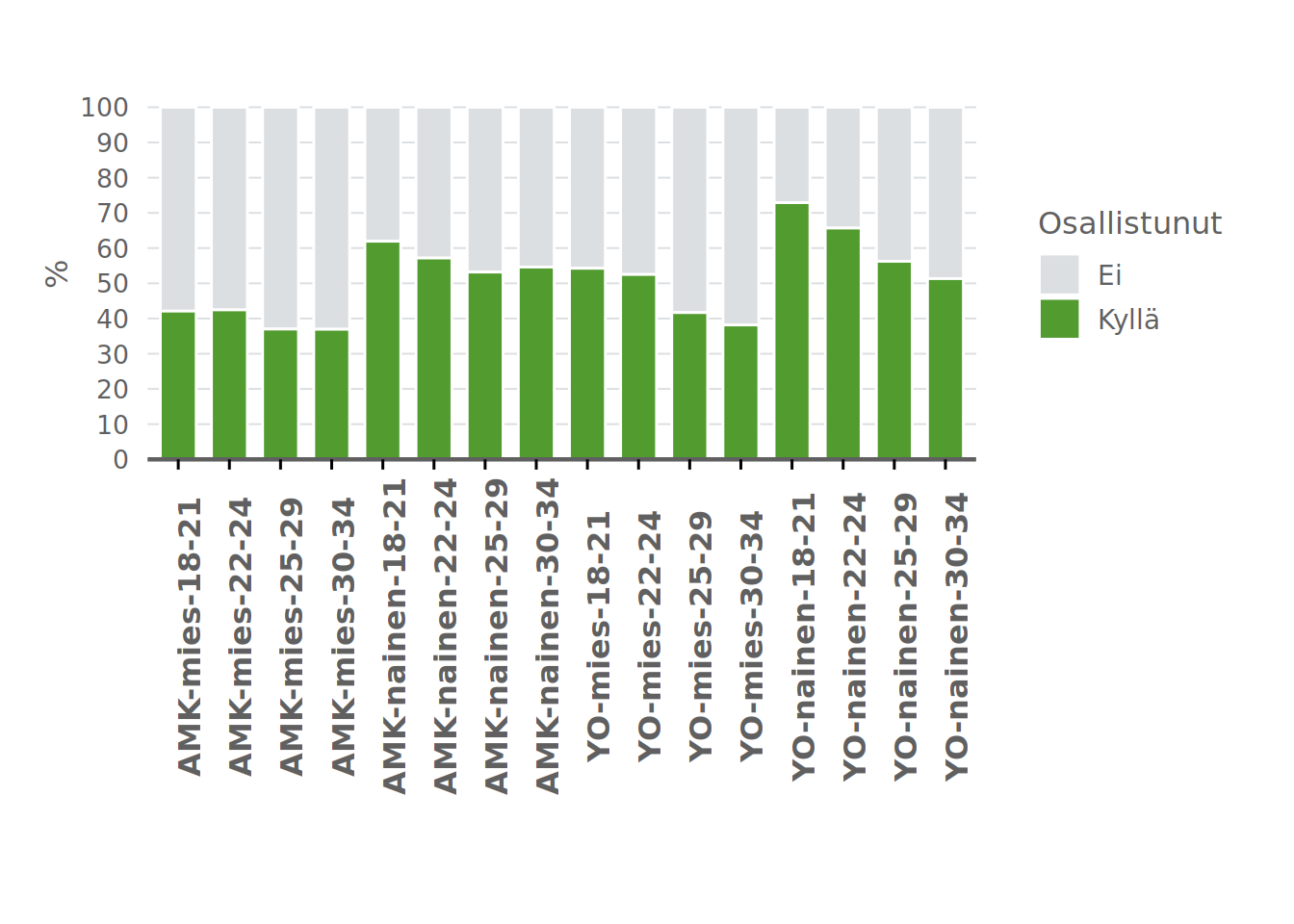
Painokertoimien taustaa: menetelmä
- KOTT 2021-aineiston painokertoimet on muodostettu käyttämällä logistiseen regressiomalliin perustuvaa käänteistodennäköisyyspainotusta (IPW)
- Painokertoimissa huomioitu otanta ja kato (kadon huomioimisessa käytetty koko otokselle saatavilla olleita rekisteritietoja)
- Painot on skaalattu siten, että niillä voidaan laskea koko korkeakouluopiskelijaväestöä edustavia tuloksia (painoissa vain yksi osite)
Otanta-asetelman kuvaavat muuttujat aineistossa
- Osite rg_stratum
- Analyysipaino w_analysis
- Väkiluku ositteessa (perusjoukon koko) rg_n
- Korottava paino w_expansion
| library(survey) svy_data <- svydesign(id = ~1, fpc = ~rg_n, weights = ~w_analysis, strata = ~rg_stratum, data = my_kott_data) |
|---|
Perustunnuslukujen laskeminen R:n survey -kirjastolla
- survey-kirjastossa määritellyt, otanta-asetelman huomioivat funktiot alkavat usein svy-etuliitteellä
- Esim. terveysliikuntasuosituksen saavuttavien osuus: kyseessä 0/1-indikaattorimuuttuja, joten keskiarvo vastaa suosituksen saavuttavien osuutta
| mean | SE | |
|---|---|---|
| ko_phexcer_guidel_enough | 0.45882 | 0.0073 |
| sukupuoli | sektori | ko_phexcer_guidel_enough | se | |
| mies.AMK | mies | AMK | 0.4592865 | 0.01742213 |
| nainen.AMK | nainen | AMK | 0.4004112 | 0.01332063 |
| mies.YO | mies | YO | 0.5082608 | 0.01598546 |
| nainen.YO | nainen | YO | 0.4701527 | 0.01221499 |
| # vain tietty sektori ja sukupuoli svymean(~ko_phexcer_guidel_enough, design=subset(svy_data, sektori=="AMK" & sukupuoli=="mies"), na.rm=T) |
|---|
| mean | SE | |
|---|---|---|
| ko_phexcer_guidel_enough | 0.45929 | 0.0174 |
Perustunnusluvut osajoukoittain thlSvyprops
| # THL:n R-paketeilla (THL:n sisäinen) osuudet ja luottamusvälit: library(thlVerse) # huom. funktion dokumentaatio ?thlSvyprops # esim. sukupuolen ja sektorin mukaan thlStats::thlSvyprops(ko_phexcer_guidel_enough~sukupuoli+sektori, svy_data) |
| ko_phexcer_guidel_enough sukupuoli sektori n_strata n_total Est lowercl_95 uppercl_95 1 0 mies AMK 637.2966 1178.621 54.1 51.2 56.9 2 0 mies YO 590.9716 1201.799 49.2 46.3 52.0 3 0 nainen AMK 794.5045 1325.082 60.0 57.3 62.6 4 0 nainen YO 815.5690 1539.253 53.0 50.5 55.5 5 1 mies AMK 541.3249 1178.621 45.9 43.1 48.8 6 1 mies YO 610.8273 1201.799 50.8 48.0 53.7 7 1 nainen AMK 530.5778 1325.082 40.0 37.4 42.7 8 1 nainen YO 723.6839 1539.253 47.0 44.5 49.5 n_strata_unweighted n_total_unweighted 1 487 896 2 510 1080 3 888 1480 4 924 1783 5 409 896 6 570 1080 7 592 1480 8 859 1783 |
|---|
Lineaarinen regressioanalyysi : svyglm
| # huom. luokitellut muuttujat määritellään tarvittaessa # käyttämällä factor()-funktiota mod1 <- svyglm(kott_weight_kg ~ kott_height_cm + factor(agegroup4), design=svy_data) summary(mod1) |
|---|
| Call: Survey design: Coefficients: (Dispersion parameter for gaussian family taken to be 195.3857) Number of Fisher Scoring iterations: 2 |
|---|
Lineaarinen regressioanalyysi : Waldin testi
| Wald test for factor(agegroup4) in svyglm(formula = kott_weight_kg ~ kott_height_cm + factor(agegroup4), design = svy_data) F = 42.9326 on 3 and 6098 df: p= < 2.22e-16 |
|---|
regTermTest(mod1, method = "Wald", ~factor(agegroup4))
- Waldin testin nollahypoteesi on, että kaikkien annettujen selittäjien (tässä siis pelkkä ikäryhmä) vaikutukset ovat nollia, eli tässä tapauksessa, että ikäryhmien välillä ei olisi eroa
- pieni p-arvo viittaa siihen, että ikäryhmien välillä on eroa
Logistinen regressiomalli : svyglm
| # logistinen regressiomalli: svyglm-funktioon argumentiksi ”family = quasibinomial()” #huom. yhdysvaikutus kuvataan :- tai *-merkinnällä, jälkimmäinen muodostaa myös päävaikutustermit mod2 <- svyglm(ko_phexcer_guidel_enough ~ factor(sukupuoli)*factor(sektori), design=svy_data, family = quasibinomial()) summary(mod2) |
|---|
| Call: Survey design: Coefficients: (Dispersion parameter for quasibinomial family taken to be 1.00129) Number of Fisher Scoring iterations: 4 |
|---|
Lopuksi
- Painokertoimien käyttäminen on välttämätöntä otannan (ja kadon) huomioimiseksi
- Lisää ohjeita THL:n survey -aineistojen käytöstä eri tilasto-ohjelmissa
- Kommentit ja kysymykset tähän ohjeeseen liittyen: kott-info(at)thl.fi



